一
公历十一月二十五日,也就是我发觉OJ上更了一道冒泡排序的那一天,我只在机房里探寻py之法,遇见泳良君,前来问我道:“可曾A了首题否?”我后悔万分,小声说道:“没有”。他就正告我其 $ O(n) $ 之算法,“先生明年还是继续努力吧。”
这我是明白的,但凡我写的题目,大概是因思维短路或细节错误,$ AC $ 的概率一向就甚为寥落,然而在这样的艰难前行中,毅然支持我的就有他。我也早就觉得该做些什么,写些什么了。
他又与我谈起文化课之苦恼,也一直觉得落下了什么。这一旬岁月的波涛汹涌,又在我的脑海里打转。积累了太多的想法,我终能确定有写一些什么的必要了。
二
但是又从何谈起呢。如同乱码一样的大脑,终究要怎么解码呢...
任何一个伟大的思想,都有一个微不足道的开始。
不如回到最初,从最基础的排序算法开始。
三
那就让我们从起点开始,重新学习,重新开始吧。
冒泡排序
冒泡排序(英语:Bubble sort)是一种简单的排序算法。由于在算法的执行过程中,较小的元素像是气泡般慢慢「浮」到数列的顶端,故叫做冒泡排序。——OI wiki 如是说
作为最简单的排序算法之一,冒泡排序就像 $ Abandon $ 在单词书里出现的感觉一样,每次都在第一页第一位,所以最熟悉。
总之在一个绝对接触不到水的课程上,这确乎是一个非常 $ 水 $ 的算法了。
光说不做可没有用
它的工作原理是每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了。
显然,每一轮排序都会把最小(大)值放在数组的最前(后)面,所以 $ n - 1 $ 轮排序后就变成了一个有序的序列了
伪代码如下:
|
1 2 3 4 5 6 7 8 9 |
函数 冒泡排序 输入 一个数组名称为array 其长度为length i 从 0 到 (length - 1) j 从 0 到 (length - 1 - i) 如果 array[j] > array[j + 1] 交换 array[j] 和 array[j + 1] 的值 如果结束 j循环结束 i循环结束 函数结束 |
很完美是吧,就像图中的一样。
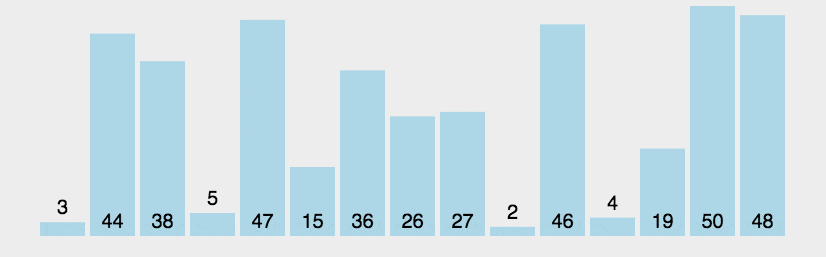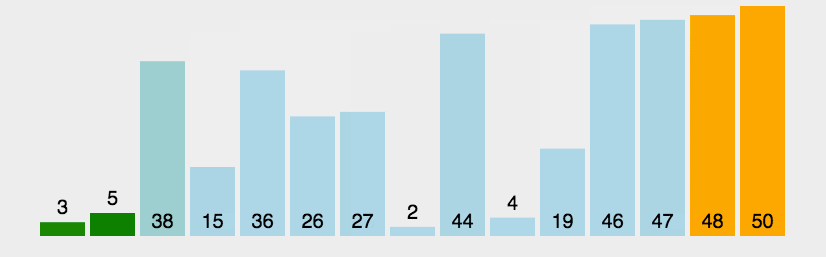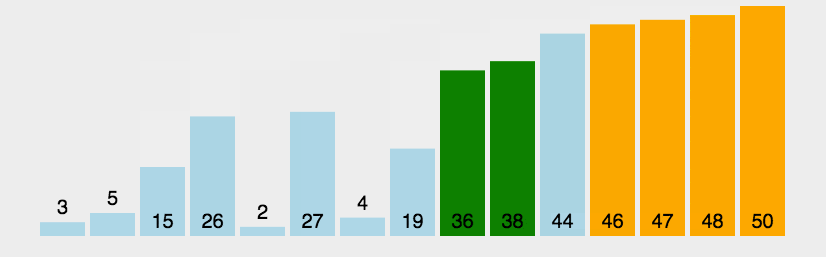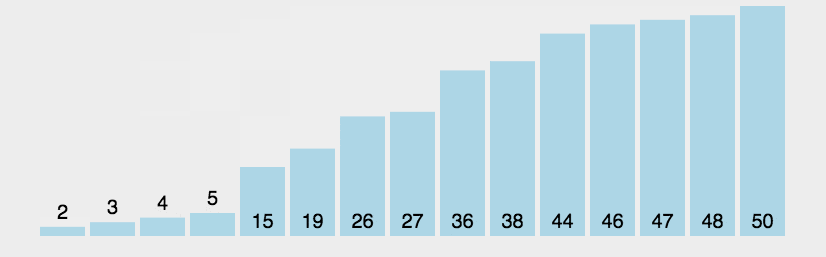
但是,我们其实会发现这样的效率其实比较低。为什么呢?
在最坏的情况,冒泡排序需要 $ O(n^{2}) $ 次交换。冒泡排序的实现通常会对已经排序好的数列拙劣地执行 $ O(n^{2}) $ 次交换。
冒泡排序如果能在内部循环第一次执行时,使用一个旗标来表示有无需要交换的可能,就可以把最优情况下的复杂度降低到 $ O(n) $。在这个情况,已经排序好的数列就无交换的需要。若在每次走访数列时,把走访顺序反过来,也可以稍微地改进效率。有时候称为鸡尾酒排序,因为算法会从数列的一端到另一端之间穿梭往返。
$ AC\ code $
c艹
偶然间看见自己在高一时写的冒泡排序,还记得那时还是 $ WJM $ 学长教我算法呢
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#include<bits/stdc++.h> using namespace std; int main(){ int a[30],n;cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; } for(int i=1;i<n;i++){ // 第一层循环表示循环次数 for(int j=n;j>1;j--) // 从后往前冒 if(a[j]>a[j-1]) // 如果逆序就交换 swap(a[j],a[j-1]); } /***************************** for(int i=1;i<n;i++){ for(int j=1;j<=n-i;j++) // 从前往后冒 if(a[j]<a[j+1]) swap(a[j],a[j+1]); *****************************/ for(int i=1;i<=n;i++) printf("%d ",a[i]); } |
PY
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
a = list(map(int, input().split())) n = len(a) c = 0 d = 0 for i in range(n - 1): flag = True for j in range(n - 1, i, -1): c += 1 if (a[j] < a[j - 1]): flag = False a[j], a[j - 1] = a[j - 1], a[j] d += 1 if (flag): # 如果有序就退出 break print(a) print(f'共比较{c}次,交换{d}次') |

发表回复